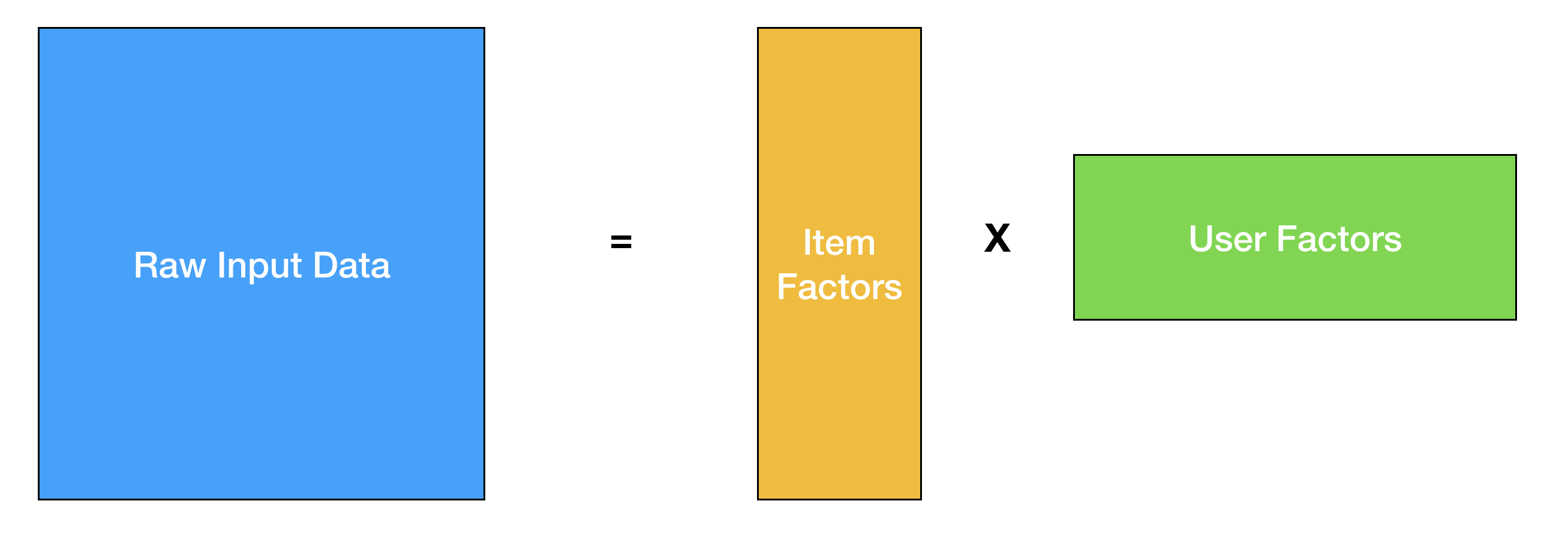
A Case For Embeddings In Recommendation Problems
Once you have worked on different machine learning problems, most things in the field start to feel very similar. You take your raw input data, map it to a different latent space with fewer dimensions, and then perform your classification/regression/clustering. Recommender systems, new and old, are no different. In the classic collaborative filtering problem, you factorize your partially filled usage matrix to learn user-factors and item-factors, and try to predict user ratings with a dot-product of the factors.